Embark on an educational journey with our comprehensive Solving Compound Inequalities Worksheet Answers, meticulously crafted to enhance your understanding of this fundamental mathematical concept. Dive into a world of inequalities, where “and” and “or” intertwine to create a captivating puzzle.
Within this worksheet, you will encounter a spectrum of problems designed to challenge your analytical skills and deepen your comprehension of compound inequalities. Guided by clear instructions, you will navigate through the intricacies of these mathematical expressions, mastering the art of solving them with precision and confidence.
1. Introduction to Compound Inequalities: Solving Compound Inequalities Worksheet Answers
Compound inequalities involve two or more inequalities connected by the words “and” or “or”. They represent a set of solutions that satisfy all or some of the component inequalities.The key difference between “and” and “or” inequalities lies in the solution set.
“And” inequalities require the solution to satisfy both component inequalities, resulting in a narrower solution set. On the other hand, “or” inequalities allow the solution to satisfy either one or both component inequalities, resulting in a wider solution set.For example, the compound inequality x > 2 and x < 5 represents all values of x that are greater than 2 and less than 5. The solution set is 3, 4. In contrast, the compound inequality x > 2 or x < 5 represents all values of x that are greater than 2 or less than 5. The solution set is (-∞, 2) ∪ (5, ∞).
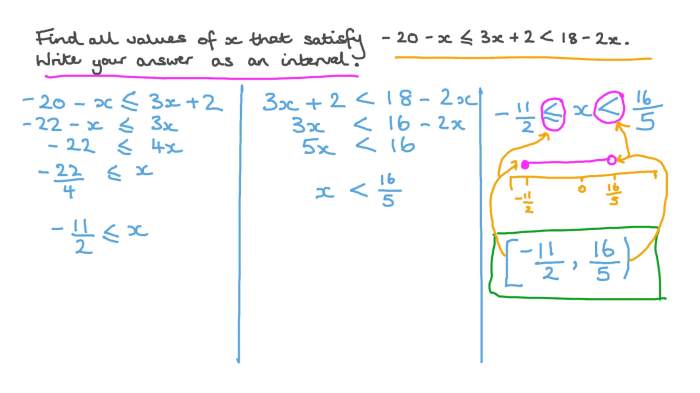
2. Solving Compound Inequalities, Solving compound inequalities worksheet answers
Solving compound inequalities involves isolating the variable on one side of the inequality and simplifying the expression.
The properties of inequalities, such as the addition and multiplication properties, can be used to simplify the solution process.To solve a compound inequality, follow these steps:
- Simplify each component inequality by isolating the variable.
- Combine the component inequalities using the appropriate conjunction (“and” or “or”).
- Solve the resulting inequality for the variable.
For example, to solve the compound inequality 2x + 1 > 5 or 3x
2 < 4, we simplify each component inequality
2x + 1 > 5
x > 4
x > 2
x
– 2 < 4 3x < 6 x < 2 Combining the component inequalities using "or", we get: x > 2 or x < 2 This compound inequality has no solution because the solution sets of the component inequalities do not overlap.
Question & Answer Hub
What is the difference between “and” and “or” inequalities?
In “and” inequalities, both conditions must be true, while in “or” inequalities, only one condition needs to be true.
How do I solve a compound inequality with “and”?
Find the intersection of the solutions to the individual inequalities.
How do I solve a compound inequality with “or”?
Find the union of the solutions to the individual inequalities.